在统计学中,“SE” 通常有以下两种主要含义:
一、标准误差(Standard Error)
定义:标准误差是样本统计量的标准差,用来衡量样本统计量的抽样误差。例如,样本均值的标准误差是用来衡量样本均值与总体均值之间的差异程度。
计算方法:
对于样本均值的标准误差,计算公式为总体标准差除以样本容量的平方根,即
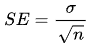
,其中σ是总体标准差,n是样本容量。
如果总体标准差未知,可以用样本标准差s来估计,此时计算公式变为
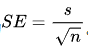
作用:
反映样本统计量的稳定性和可靠性。标准误差越小,说明样本统计量对总体参数的估计越准确、越可靠。
在参数估计中,用于构建置信区间。例如,对于总体均值的估计,通常使用样本均值加减一定倍数的标准误差来确定置信区间。
在假设检验中,用于计算检验统计量。例如,在进行 t 检验时,检验统计量
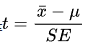
,其中元是样本均值,μ是总体均值,SE是样本均值的标准误差。
二、标准误(Standard Error of Estimate)
定义:在回归分析中,标准误是衡量回归方程对观测值拟合程度的指标。它表示实际观测值与回归方程预测值之间的平均差异程度。
计算方法:
对于简单线性回归模型
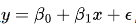
,标准误的计算公式为
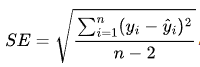
,其中yi是实际观测值,yi是回归方程预测值,n是样本容量。
作用:
评估回归模型的精度。标准误越小,说明回归方程对观测值的拟合程度越好,预测值越准确。
进行假设检验。可以通过比较回归系数与标准误的比值来进行假设检验,判断回归系数是否显著不为零。
总之,在统计学中,“SE” 通常表示标准误差或标准误,具体含义取决于使用的场景。理解和正确计算 “SE” 对于进行准确的统计分析和推断非常重要。