在矩阵中，k 阶子式是指从一个矩阵中选取 k 行和 k 列，由这些行与列交叉处的元素所构成的行列式。
一、具体解释
行数和列数的选择
从矩阵的众多行中任选 k 行，同时从众多列中任选 k 列。
选择的方式是多样的，不同的选择会得到不同的 k 阶子式。
构成行列式
选定 k 行和 k 列后，位于这些行与列交叉处的元素按照行列式的定义构成一个 k 阶行列式。
行列式的计算方法是根据特定的规则，例如对于二阶行列式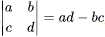
。
二、举例说明
设矩阵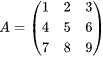
。
二阶子式
比如选取矩阵A的第一行和第二行，以及第一列和第二列，得到的二阶子式为
，计算这个二阶子式的值为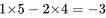
。
三阶子式
矩阵A本身就是一个三阶子式，其值为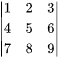
，计算过程相对复杂，但可以通过按行（列）展开等方法来计算。
三、作用和意义
矩阵的秩的确定
通过计算不同阶数的子式是否为零，可以确定矩阵的秩。如果存在一个 k 阶子式不为零，而所有高于 k 阶的子式全为零，那么矩阵的秩就是 k。
线性方程组的解的判断
在研究线性方程组的解的结构时，矩阵的子式起着重要的作用。例如，通过判断系数矩阵的某些特定子式是否为零，可以确定线性方程组是否有唯一解、无穷多解或无解。