标准差公式是用来衡量一组数据离散程度的数学表达式。
标准差的公式为：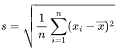
。
其中，s表示标准差;n是数据的个数;xi表示第i个数据值;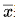
表示这组数据的平均数。
具体解释如下：
先计算平均数：
将一组数据中的所有数值相加，然后除以数据的个数n，得到这组数据的算术平均值。例如，对于数据3、5、7，平均数为(3+5+7)÷3=5。
计算每个数据与平均数的差值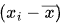
：
用每个数据值减去平均数，得到每个数据与平均数的偏差。例如，对于数据3、5、7，与平均数5的差值分别为3-5=-2，5-5=0，7-5=2。
对差值进行平方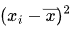
：
将上述得到的差值进行平方，目的是消除差值的正负号影响，同时放大偏差较大的数据的影响。例如，上述差值平方后为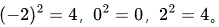
求平方后的差值的平均数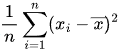
：
将所有平方后的差值相加，再除以数据个数n，得到这些平方差值的平均数。例如，对于上述数据，平方差值的平均数为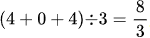
。
最后求平方根得到标准差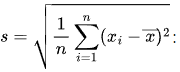
对上述平方差值的平均数开平方，得到标准差。对于上述例子，标准差为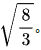
标准差越大，说明数据的离散程度越大，即数据分布越分散；标准差越小，说明数据的离散程度越小，即数据分布越集中。