在 Excel 中，标准差是用来衡量一组数据的离散程度的统计量。
具体来说:
一、概念解释
1.标准差数值大小反映了数据的波动情况:
标准差大，表示数据分散程度大，数据点相对比较远离平均值，波动较大。
标准差小，表示数据比较集中在平均值附近，波动较小。
2.与平均值的关系:
标准差的计算是基于数据与平均值的差异。它通过计算每个数据点与平均值的偏差的平方和的平均数的平方根得到。
二、计算公式及示例
在 Excel 中，使用函数可以快速计算标准差。
1.总体标准差函数为STDEVP :假设数据在A1:A10单元格区域，在Excel中可以输入公式=STDEVP(A1:A10)来计算总体标准差。
例如，数据为{2,4,6,8,10}，首先计算平均值为(2+4+6+8+10)÷5=6。
然后计算每个数据点与平均值的偏差的平方和:(2 - 6)² +(4-6)²+(6-6)²+(8- 6)² +(10 - 6)² = 40。
接着计算偏差的平方和的平均数为40÷5=8。
最后，总体标准差为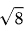
≈2.828。
2.样本标准差函数为STDEV:同样假设数据在A1:A10单元格区域，可输入公式=STDEV(A1:A10)来计算样本标准差。样本标准差的计算方法与总体标准差类似，但在计算偏差的平方和的平均数时，除数为n-1(n为数据个数)，而总体标准差的除数是n。
三、实际应用场景
1.质量控制:在制造业中，标准差可以用来衡量产品质量的稳定性。如果生产过程中测量的数据标准差较小，说明产品的质量比较稳定，生产过程处于良好的控制状态;反之，如果标准差较大，可能需要检查生产过程是否存在问题，以便及时调整。
2.金融分析:在金融领域，标准差常用于衡量投资组合的风险。投资组合的收益率的标准差越大，说明投资风险越高;标准差越小，说明投资风险相对较低。
3.教育评估:在教育领域，可以用标准差来分析学生考试成绩的分布情况。如果成绩的标准差较小，说明学生的成绩比较集中，教学效果可能比较均衡;如果标准差较大，可能需要进一步分析教学中存在的问题，以便采取针对性的措施提高教学质量。