在数学中,“x”通常有以下几种主要的意思:
一、作为未知数
1.方程中的未知数
在方程中,“x”常被用来代表一个未知的数量。例如在方程2x+5=11中,"x”就是我们要求解的未知数。通过各种运算方法,我们可以确定“x”的值,在这个例子中,解得x=3.
它可以表示任何未知的数值,无论是整数、分数、小数还是无理数等。其作用是让我们通过已知的条件和数学运算规则去找出这个未知量,从而解决问题。
2.函数中的变量
在函数中,“x”通常作为自变量出现。例如在函数y =f(x)中,"x”的取值决定了函数y的值。不同的函数关系会根据“x”的变化而产生不同的y值。
比如在一次函数y=2x+1中,当x取不同的值时,对应的y值也会随之变化。这里的“x”可以代表任何实数,通过改变“x”的值,我们可以观察函数的变化趋势和性质。
二、作为参数或变量的通用符号
1.表示一般的数值变量
在数学表达式和公式中,“x”常被用作一个通用的变量符号,可以代表各种不同的数值。例如在代数式ax² + bx + c中,“x"可以取任意实数,而a、b、c是常数。
这种用法使得数学公式具有通用性,可以适用于各种不同的具体情况。只需要给定“x”的具体值,就可以计算出表达式的值。
2.作为参数参与运算
在一些数学运算和定理中,“X”可以作为一个参数出现。例如在三角函数中,sin(x)、cos(x)等,“x)表示角度或弧度值,函数根据“x”的值计算出对应的正弦、余弦值。
又如在极限运算中,
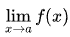
,“x"作为变量趋向于某个值a,用来研究函数在特定趋势下的行
为。
三、在几何中的含义
1.表示坐标轴上的变量
在平面直角坐标系中,“x”通常代表横坐标。一个点的位置可以用有序数对(x,y)来表示,其中“x”确定了点在水平方向上的位置。
例如点(3,4)中,“x=3) 表示这个点在x轴上的位置是3个单位长度。通过"x"和“y”的值,可以确定平面上任意一点的位置。
2.几何图形中的参数
在几何图形的方程和公式中,“x”也可以作为参数出现。例如在圆的方程(x -a)² +(y-b)²= r²中,“x” 和“y) 是坐标变量,a、b是圆心的坐标,r是半径。通过改变“x”和“y”的值,可以确定圆上的不同点。
在椭圆、双曲线等其他几何图形的方程中,“x”同样扮演着重要的角色,作为变量参与图形的定义和描述。