标准差是用来衡量一组数据离散程度的统计量。
一、定义及计算公式
定义：标准差是一组数据平均值分散程度的一种度量。一个较大的标准差，代表大部分数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。
计算公式：
假设一组数据为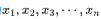
，这组数据的平均数为
。
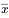先计算每个数据与平均数的差的平方，即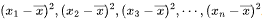
。
再求这些平方差的平均数，即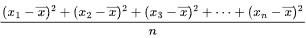
。
最后对这个平均数开平方，得到的结果就是标准差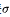
，即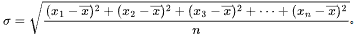
。
二、实际意义及应用场景
在数据分析中的意义：
反映数据的波动情况：如果一组数据的标准差较大，说明这组数据的波动较大，各个数据之间的差异较为明显；如果标准差较小，则说明数据比较集中，波动较小。
例如，在股票市场中，某只股票价格在一段时间内的标准差较大，说明该股票价格波动剧烈，风险相对较高；而标准差较小的股票价格则相对稳定。
帮助判断数据的可靠性：标准差可以用来评估数据的可靠性。如果多次测量或抽样得到的数据标准差较小，说明数据的稳定性较高，测量结果较为可靠；反之，如果标准差较大，则可能需要重新检查测量方法或数据来源。
比如，在科学实验中，对同一物理量进行多次测量，如果测量结果的标准差较小，说明实验的精度较高，结果较为可靠。
不同领域的应用场景：
金融领域：
风险评估：在投资组合管理中，标准差被广泛用于衡量投资风险。投资组合的标准差越大，意味着投资收益的波动越大，风险也就越高。
例如，假设有两个投资组合 A 和 B，A 组合的标准差为 10%，B 组合的标准差为 15%。在其他条件相同的情况下，B 组合的风险相对较高，因为其收益的波动幅度更大。
资产定价：在资本资产定价模型（CAPM）中，标准差也是一个重要的参数。它用于衡量单个资产或投资组合相对于市场的风险程度，从而确定资产的预期收益率。
工业生产领域：
质量控制：在生产过程中，标准差可以用来监控产品质量的稳定性。通过计算产品关键指标的标准差，可以判断生产过程是否处于稳定状态。
例如，在汽车制造中，对发动机的关键尺寸进行测量，如果这些尺寸的标准差在可接受范围内，说明生产过程稳定，产品质量可靠；如果标准差超出了控制限，可能需要调整生产工艺或设备，以确保产品质量。
性能评估：对于一些性能指标要求较高的产品，如电子产品的性能参数，可以通过计算标准差来评估产品性能的一致性。标准差越小，说明产品性能越稳定，质量越好。
教育领域：
学生成绩分析：在教育评估中，标准差可以用来分析学生成绩的分布情况。如果学生成绩的标准差较大，说明学生之间的成绩差异较大，教学效果可能存在较大的差异；如果标准差较小，说明学生成绩较为集中，教学效果相对较为均衡。
例如，在一次考试中，某班级学生的数学成绩标准差为 10 分。如果该班级学生人数较多，标准差为 10 分可能意味着学生成绩分布较为分散，教师可以进一步分析成绩差异的原因，以便调整教学方法。
教学质量评估：标准差也可以用于评估教学质量的稳定性。通过对多次考试成绩的标准差进行分析，可以判断教学质量是否稳定，是否需要改进教学方法或调整教学内容。
统计学研究领域：
假设检验：在假设检验中，标准差是计算检验统计量的重要参数之一。通过比较样本标准差与总体标准差的差异，可以判断样本是否来自于特定的总体分布。
例如，在对两个样本的均值进行比较时，可以通过计算两个样本的合并标准差，来确定检验统计量的值，从而判断两个样本的均值是否存在显著差异。
置信区间估计：在参数估计中，标准差用于计算置信区间的宽度。置信区间是在一定置信水平下，对总体参数的估计范围。标准差越大，置信区间的宽度也越大，估计的精度就越低。
比如，在对总体均值进行估计时，如果已知样本标准差较大，那么为了达到相同的置信水平，需要更大的样本量才能获得更精确的估计结果。