标准分是一种由原始分推导出来的相对地位量数，它是用来说明原始分在所属的那批分数中的相对位置的。
一、计算方法
标准分的计算通常有两种方法：Z 分数法和 T 分数法。
Z 分数法：
Z 分数也称为标准分数，是以标准差为单位来衡量某一原始分数与平均数之间的距离。
计算公式为：Z=(X-\overline {X})/S，其中 X 是原始分数，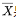
是平均数，S 是标准差。
例如，某学生在一次考试中数学成绩为 85 分，全班平均成绩为 75 分，标准差为 5。那么该学生的数学成绩标准分为 Z=(85 - 75)/5 = 2。
T 分数法：
由于 Z 分数可能会出现负数，且数值可能比较小，不太方便理解和使用。因此，常常将 Z 分数进行线性变换，得到 T 分数。
计算公式为：T = aZ + b，其中 a 和 b 是常数，通常取 a = 10，b = 50。这样，T 分数的平均数为 50，标准差为 10。
继续以上面的例子，该学生的 Z 分数为 2，那么他的 T 分数为 T = 10×2 + 50 = 70。
二、实际意义及应用场景
教育领域：
学生成绩评估：在教育领域，标准分常被用于评估学生的考试成绩。通过将学生的原始分数转换为标准分，可以更准确地了解学生在班级或群体中的相对位置。
例如，在高考中，不同科目的难度和考生群体不同，直接比较原始分难以客观评价考生的综合水平。而使用标准分，可以将不同科目的成绩进行统一比较，使得录取更加公平。
教学质量分析：标准分也可以用于分析教学质量。通过比较不同班级或学校学生的标准分，可以了解教学效果的差异，为教学改进提供依据。
比如，两个学校的学生在同一次考试中的原始分可能差异较大，但通过计算标准分，可以更客观地比较两个学校的教学质量。
心理测量领域：
智力测验和人格测验：在心理测量中，标准分被广泛应用于各种智力测验和人格测验。这些测验的结果通常以标准分的形式呈现，以便更好地理解个体在相应特质上的表现水平。
例如，韦氏智力测验的结果就是以标准分表示的，平均数为 100，标准差为 15。通过比较个体的标准分与平均数的差异，可以判断其智力水平在人群中的位置。
心理评估和诊断：标准分还可以用于心理评估和诊断。一些心理量表的得分经过标准化处理后，可以更准确地判断个体是否存在心理问题以及问题的严重程度。
比如，在抑郁症的评估中，常用的抑郁自评量表的得分可以转换为标准分，根据标准分的范围来判断个体的抑郁程度。
统计分析领域：
数据比较和分析：在统计分析中，标准分可以用于比较不同数据集的分布情况。通过将不同数据集的原始数据转换为标准分，可以在同一尺度下进行比较，从而更好地理解数据的特征和差异。
例如，比较两个不同地区的居民收入水平时，如果直接比较原始收入数据可能会受到地区经济发展水平等因素的影响。而将收入数据转换为标准分后，可以更客观地比较两个地区居民收入在各自总体中的相对位置。
异常值检测：标准分还可以用于检测数据中的异常值。一般来说，标准分大于 3 或小于 -3 的数据点可能被视为异常值，需要进一步检查和分析。
比如，在一组学生的考试成绩中，如果某个学生的标准分远高于或远低于其他学生，那么这个学生的成绩可能存在异常，需要检查是否存在作弊或其他特殊情况。