标准差是用来衡量一组数据离散程度的统计量。“2 个标准差” 通常有以下含义:
一、数学定义及计算
首先回顾一下标准差的计算方法。
假设一组数据为
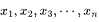
,这组数据的平均数为
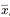
。
先计算每个数据与平均数的差的平方,即
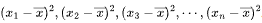
。
再求这些平方差的平均数,即
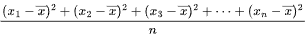
。
最后对这个平均数开平方,得到的结果就是标准差
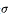
,即
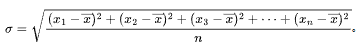
。
“2 个标准差” 的含义。
如果以平均数为中心,“2 个标准差” 就是在平均数的基础上,向上或向下分别加上或减去 2 倍的标准差。即范围在
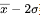
到
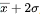
之间。
二、实际意义及应用场景
在数据分析中的意义:
反映数据的分布范围:“2 个标准差” 可以大致确定数据的分布范围。在正态分布中,约有 95% 的数据会落在平均数加减 2 个标准差的范围内。这意味着如果数据服从正态分布,那么在这个范围内的数据占比很高,超出这个范围的数据相对较少。
例如,在学生考试成绩的统计中,如果平均分为 70 分,标准差为 5 分,那么 “2 个标准差” 的范围就是 60 分(70 - 2×5)到 80 分(70 + 2×5)。大约 95% 的学生成绩会落在这个范围内。
评估数据的异常值:如果一个数据点超出了 “2 个标准差” 的范围,那么在很多情况下可以认为这个数据点是异常值。异常值可能是由于测量错误、数据录入错误或者特殊情况导致的。通过识别异常值,可以对数据进行进一步的检查和处理,以提高数据的质量。
比如在生产过程中,对产品的某个关键尺寸进行测量,如果某个测量值超出了平均数加减 2 个标准差的范围,那么就需要对这个产品进行进一步的检查,以确定是否存在质量问题。
在不同领域的应用场景:
金融领域:
风险评估:在投资组合管理中,标准差被广泛用于衡量投资风险。“2 个标准差” 可以作为一个风险衡量的参考指标。例如,如果一个投资组合的预期收益率为 10%,标准差为 5%,那么在正态分布的假设下,大约有 95% 的概率该投资组合的收益率会落在 0%(10% - 2×5%)到 20%(10% + 2×5%)之间。这可以帮助投资者了解投资组合的潜在风险范围。
信用评级:在信用风险评估中,标准差也可以用来衡量债务人的违约风险。“2 个标准差” 可以作为一个判断信用风险的阈值。如果一个债务人的财务指标(如资产负债率、流动比率等)的波动超出了一定的范围(例如 2 个标准差),那么可能意味着该债务人的信用风险较高。
质量管理领域:
过程控制:在生产过程中,通过对关键质量指标的监测和控制,可以确保产品质量的稳定性。“2 个标准差” 可以作为过程控制的上下限。如果生产过程中的质量指标超出了 “2 个标准差” 的范围,那么就需要对生产过程进行调整,以确保产品质量符合要求。
质量检验:在产品质量检验中,“2 个标准差” 可以作为判断产品是否合格的依据之一。如果一个产品的某个质量指标超出了平均数加减 2 个标准差的范围,那么这个产品可能被判定为不合格品。
科学研究领域:
实验数据分析:在科学实验中,对实验数据的分析通常需要考虑数据的可靠性和准确性。“2 个标准差” 可以作为判断实验结果是否可靠的一个指标。如果实验结果的误差在 “2 个标准差” 范围内,那么通常认为这个实验结果是可靠的。
统计推断:在统计推断中,“2 个标准差” 也经常被用于确定置信区间。例如,在对总体均值进行估计时,可以根据样本数据计算出平均数和标准差,然后构建一个置信区间,通常在平均数加减一定倍数的标准差范围内(如加减 2 个标准差),这个区间可以用来估计总体均值的可能取值范围。