扩展标准差通常是在传统标准差概念基础上进行一定扩展和引申的统计量。
一、基本概念与传统标准差的关系
传统标准差:
传统标准差是用来衡量一组数据离散程度的统计量。它反映了数据点与平均数的平均距离。较小的标准差表示数据点比较集中在平均数附近,数据的离散程度小;较大的标准差则表示数据点比较分散,离散程度大。
扩展标准差的含义:
扩展标准差在一定程度上继承了传统标准差反映数据离散程度的特性,但可能会结合更多的因素或在特定的应用场景下进行了扩展。例如,可能考虑了数据的分布形态、异常值的处理方式、多变量数据的综合离散程度等。
二、可能的扩展方向及应用场景
考虑数据分布形态:
在某些情况下,仅仅使用传统标准差可能无法全面反映数据的特征。例如,如果数据呈现明显的偏态分布或尖峰厚尾分布,传统标准差可能不能准确地描述数据的离散程度。此时,可以通过引入一些调整因子或采用特定的分布模型来计算扩展标准差,以更好地适应数据的分布特点。
比如,在金融领域中,资产收益率的分布往往具有尖峰厚尾的特征,传统标准差可能低估了风险。通过使用基于极值理论或其他分布模型计算的扩展标准差,可以更准确地衡量资产收益率的波动风险。
处理异常值:
传统标准差对异常值比较敏感,一个极端的异常值可能会显著影响标准差的大小。在一些应用场景中,需要对异常值进行特殊处理或采用更稳健的统计量来计算扩展标准差。
一种常见的方法是使用中位数绝对偏差(MAD)作为稳健的离散程度度量,然后通过一定的转换得到扩展标准差。这样可以减少异常值对离散程度估计的影响,使统计量更加稳健。
例如,在工业生产过程中,如果数据中存在个别异常值,可能是由于测量误差或突发情况导致的。使用扩展标准差可以更准确地评估生产过程的稳定性,避免因异常值而错误地判断生产过程出现了严重问题。
多变量数据的应用:
对于多变量数据,传统标准差通常是分别计算每个变量的标准差,然后进行综合分析。而扩展标准差可以考虑多个变量之间的相关性和联合分布,提供一个更综合的离散程度度量。
例如,在环境科学中,同时监测多个环境指标(如温度、湿度、空气质量等)。扩展标准差可以考虑这些指标之间的相互关系,综合评估环境数据的离散程度,为环境质量评价和管理提供更全面的信息。
三、计算方法示例
基于分布模型的扩展标准差计算:
假设数据服从某种特定的分布,如 t 分布。首先估计分布的参数,然后根据分布的特性计算扩展标准差。
对于一组数据
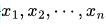
,假设它们服从自由度为的 t 分布。首先计算样本均值和样本方差
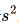
。然后,根据 t 分布的性质,扩展标准差可以计算为
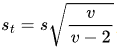
,其中
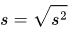
是传统标准差。
基于稳健统计的扩展标准差计算:
以中位数绝对偏差(MAD)为基础进行计算。首先计算数据的中位数M,然后计算每个数据点与中位数的绝对偏差
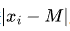
。MAD 定义为这些绝对偏差的中位数。
扩展标准差可以计算为
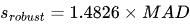
,其中 1.4826 是使得在正态分布下该统计量近似等于传统标准差的系数。
总之,扩展标准差是对传统标准差的一种扩展和改进,旨在更好地适应不同的数据特征和应用场景,提供更准确和全面的离散程度度量。