标准正态分布是一种特殊的正态分布,具有以下特点和重要意义:
定义与特征
定义:标准正态分布是均值为0、标准差为1的正态分布,通常用N(0,1)表示。
概率密度函数:其概率密度函数为
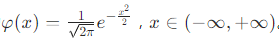
。该函数图像关于x=0对称,在x=0处取得最大值
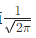
,并且随着x向正负无穷方向延伸,函数值逐渐趋近于0。
图像特点:标准正态分布的图像是一个钟形曲线,具有单峰性、对称性和渐近性。曲线在x=0两侧逐渐下降,且在x=±1处有两个拐点。
应用
标准化:任何一个一般的正态分布
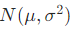
都可以通过线性变换
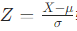
转化为标准正态分布N(0,1)。这使得对于不同均值和标准差的正态分布问题,可以统一转化为标准正态分布来进行研究和计算,大大简化了计算过程。例如,已知某班学生的考试成绩服从正态分布
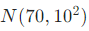
,要计算成绩在80分以上的学生所占比例,就可以先将成绩X进行标准化,得到
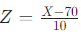
,然后通过查标准正态分布表来计算相应的概率。
统计推断:在统计学中,标准正态分布是许多统计推断方法的基础。例如,在假设检验中,当样本量较大时,一些统计量(如样本均值、样本比例等)的抽样分布近似服从标准正态分布,从而可以利用标准正态分布的性质来确定检验统计量的临界值,进而判断是否拒绝原假设。在置信区间的构造中,也常常会用到标准正态分布的分位数来确定置信区间的上下限。
重要性
理论基础:标准正态分布在概率论和数理统计的理论研究中具有核心地位。许多其他分布在一定条件下可以用标准正态分布来近似,如二项分布在n很大、p不太靠近0或1时,可近似为正态分布,进而通过标准化转化为标准正态分布进行分析。
实际应用广泛:在自然科学、社会科学、工程技术等众多领域都有广泛应用。例如,在质量管理中,用于控制产品质量的波动范围;在医学研究中,分析人体生理指标的分布情况;在经济学中,研究股票价格、利率等随机变量的变化规律等。